www.quondam.com/44/4411.htm

ongoing history of the circle-square juncture

1998.02.09
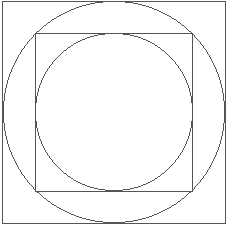
The Ongoing History of the Circle/Square Juncture
...the story begins with Serlio and the Stanza geometry article. Then comes the Canon of Polyclytus, the solar system, the Timepiece gauge, phases of the imagination as related to the internal organs. ...the Villa Rotunda/Goldenberg House study and the Timepiece of Humanity notes.

Draw a circle in a square with the diameter of the circle being equal to a side of the square. Draw another circle concentric with the first and having a diameter equal to the diagonal of the square. The second circle is twice as great in area as the first circle. Likewise, another square tangent on all sides to the greater circle is twice the area of the first square.

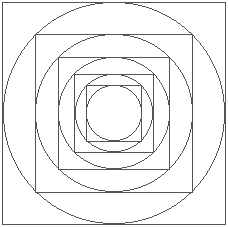
Continuing the process of drawing circles in squares, you find that the area of the outer circles and squares have a relationship of 2 to the nth power with the innermost circle and square; n being the number of circles or squares from the first circle or square.

««««

»»»»

3707 3716 3723
www.quondam.com/44 /4411.htm