98100701 ICM Officina Machina model 2110i35
2000.10.07 12:18
non-Euclidean geometry
Non-Euclidean geometry, that term oft-used but not exactly understood by many of today's non-orthogonally 'inclined' architects and theorists, stems from the many age-old mathematical attempts to disprove one of Euclid's axioms:
"There was in particular one axiom, the axiom of parallels, which they disliked and attempted to eliminate. The axiom states that through a given point one and only one parallel can be drawn with respect to a given line; that is, there is one and only one line that does not ultimately intersect with a given line and yet lies in the same plane." (from H. Reichenbach, The Rise of Scientific Philosophy, 1951.)
With the discovery that light does not travel in a straight line, the notion that parallel lines can then (eventually) intersect seems to disprove Euclid's parallel axiom.
Another aspect of non-Euclidean geometry is that the sum of the angles inside a triangle can add up to more that 180 degrees, but such triangles only truly exist when the area of the triangle is extremely vast, say a triangle created by connecting three galaxies.
Basically, it is still Euclidean geometry that governs what architects on Earth are capable of building.
As an aside, I remember reading that Gehry's office, when first dealing with designs that collaged many non-orthogonal surfaces and forms, resorted to 'descriptive geometry'.
2000.10.07 17:03
Re: geometry notes
Could it be that human perception of space may be non-Euclidean, but that human imagination has evolved (so far) in a very Euclidean manner?
051007a plans of domestic architecture 2080i12
051007b tallest.db with Empire State building corrected 2060i03
2014.10.07 21:39
7 October
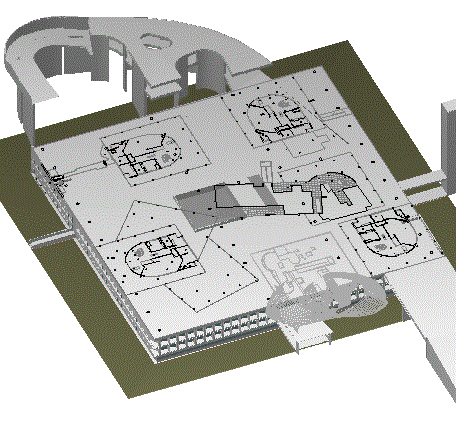
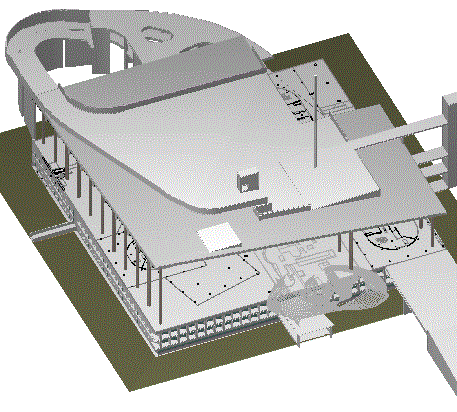
Spent a few hours today working on a model of Palais Savoye. Just about at the point now where the models of all the various Savoye derivatives can be placed within the skeleton Palais. I basically had to carve out a corner of the Palais's undulating roof plane, so, yes, lots of x, y and z manipulation.
| |
Up to now I've just been manipulating 2D data to achieve these elevations:
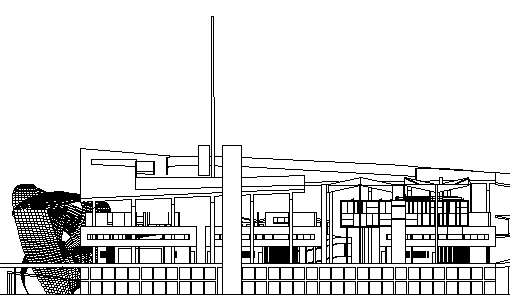
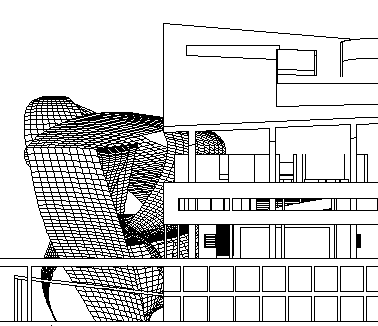
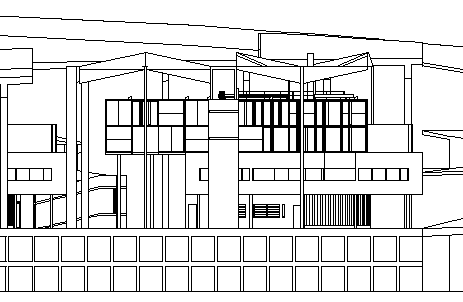
And, of course, a model will enable much more interesting views (into an otherwise virtual museum of architecture).
| |
15100701 SANAA Building at Grace Farms New Canaan
18100701 Acropolis of Contemporary Art model work 2473i04
19100701 iq32 Cubist ICM Plan Obus 2436i74
19100702 Louvre plan sections nts 207hi01
|





