history

not an easy book

  z   5   b   c   d   e   f   g   h   i   j   k   l   m   n   o   p   q   r   s   t   u   v   w   x   y   z   6

The complex oculus and other openings of the inner dome in S. Chiara, Bra, define residual space, which is open in order to elaborate space and manipulate light.
Robert Venturi, Complexity and Contradiction in Architecture (1966), p. 82.

The detachment of the inner and outer window openings in Aalto's Imatra Church similarly modifies light and space. The use of this method is unique in recent architecture.
Robert Venturi, Complexity and Contradiction in Architecture (1966), p. 82.

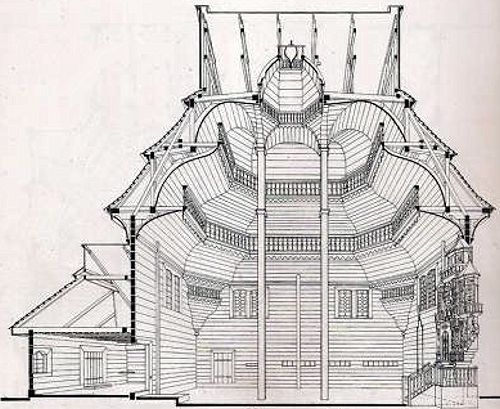
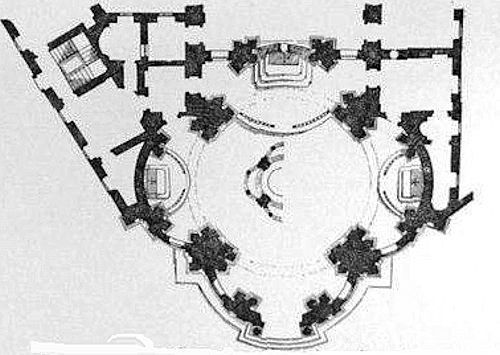
The wooden vaulting of seventeenth century Polish synagogues, which imitates masonry, makes closed linings in the upper section. In contrast to the previous examples their residual space is closed.
Robert Venturi, Complexity and Contradiction in Architecture (1966), p. 82.

««««

»»»»

www.quondam.com/45/4507o.htm

Quondam © 2020.04.16