Peter Eisenman, et al, Oppositions 12 (Cambridge, MA: The MIT Press, 1979).
Contents
Alan Colquhoun:
From Bricolage to Myth: or how to put Humpty-Dumpty together again
Peter Eisenman:
The Graves of Modernism
Alan Colquhoun:
Form and Figure
Francesco Dal Co and Sergio Polano:
Interview with Albert Speer
Kenneth Frampton:
A Synoptic View of the Architecture of the Third Reich
Gruppo Sette:
Architecture: Unpreparedness -- Incomprehension -- Prejudice
Architecture: A New Archaic Era
Atheneum 2231
1975-79
Brant House Addition 223b
Museum of Arts and Crafts 2244
Peter Eisenman, et al, Oppositions 13 (Cambridge, MA: The MIT Press, 1979).
Contents
Francesco Dal Co:
Criticism and Design
Anthony Vidler:
Postscript
Rafael Moneo:
On Typology
Georges Teyssot:
Emil Kaufmann and the Architecture of Reason: Klassizismus and "Revolutionary Architecture"
Joachim Schlandt and O. M. Ungers:
The Vienna Superblocks
Philip Johnson, "Afterword" in Philip Johnson: Writings. New York: Oxford University press, 1979. p. 268-71.
Peter Eisenman, et al, Oppositions 14 (Cambridge, MA: The MIT Press, 1979).
Contents
Kenneth Frampton:
Mario Botta and the School of the Ticino
Alan Colquhoun:
Sign and Substance: Reflections on Complexity, Las Vegas, and Oberlin
Maurice Culot and Léon Krier:
The Only Path for Architecture
Léon Krier:
The Consumption of Culture
Georges Teyssot:
John Soane and the Birth of Style
Bruno Taut:
The Earth--A Good Home
Papal Mass (Philadelphia, PA: Logan Circle, 1979.10.03).
| |

Peter Eisenman, House X (1979).
| |
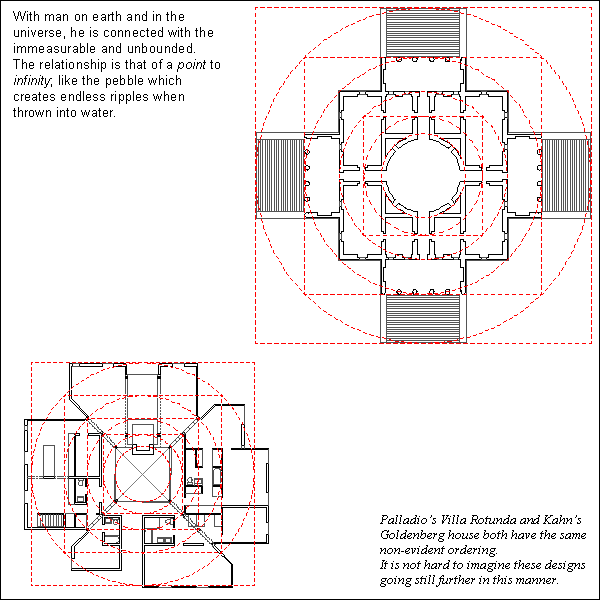
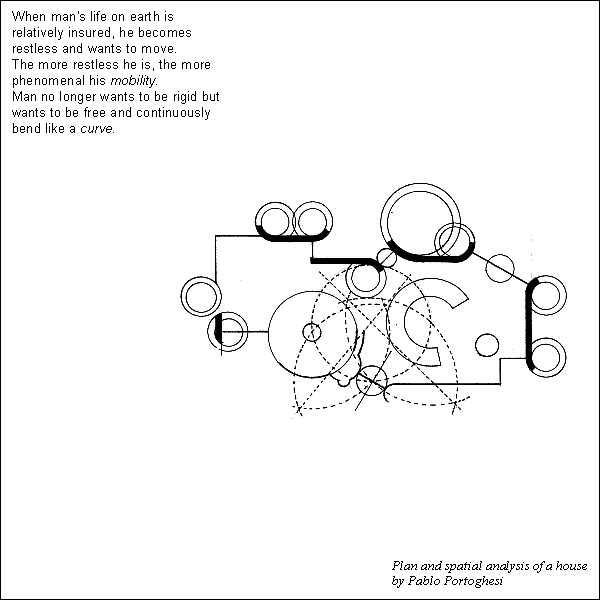
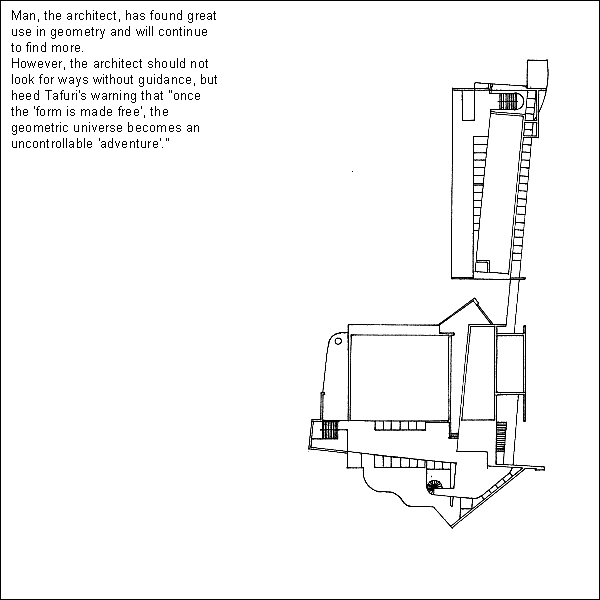
Stephen Lauf, Geometry: its internal workings, its external expression, and its meaning in architecture (Spring 1979).
Geometry is the branch of mathematics that deals with space and its relations. The word geometry is derived from two Greek words meaning earth and measure. Man was once believed to be the measure of all things and perhaps in some ways still is. In architecture, geometry and man are used together; geometry as its form and man as its measure. Through this merger, a meaning evolves. Therefore, the purpose of this article is to demonstrate both the mechanical and theoretical aspects of geometry in the realm of architecture.
The mechanical principles of geometry [used throughout the article] are from the first book of Sebastiano Serlio's Books of Architecture. The remaining text and analysis are my own.
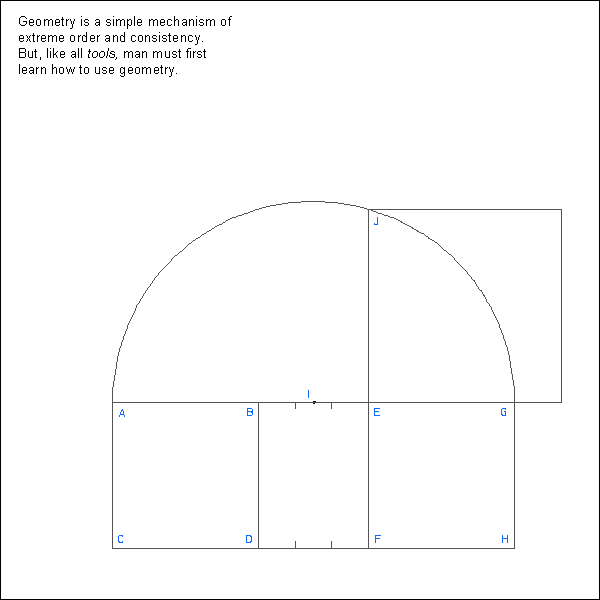
To increase the area of a square 3/4, and still retain a square, draw square ABCD. To one side of the square add 3/4 of the square creating rectangle AECF. To ACEF add a square of the same area as ABCD creating rectangle AGCH. Line AG is the diameter of the circle with the center I, which divides line BE in half. Draw semicircle AG. Extend line EF until it reaches the arc at point J. Line is one side of the new square whose area is 3/4 greater than ABCD. This formula can be used to increase a square any amount. It is also used to change any rectangle into a square.
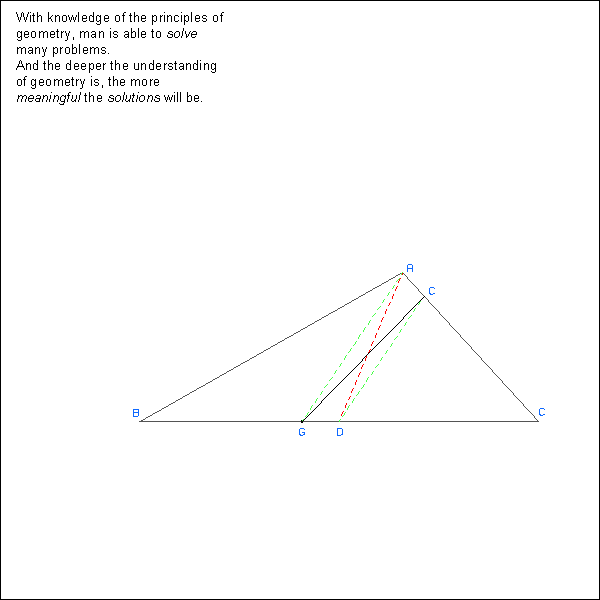
Given an irregular piece of land (triangle ABC) and a well at point G. You must divide the land equally with both parts being able to partake from the well. Bisect BC and draw AD. This divides the triangle equally but the well (point G) is only in one half. Draw line AG. From D draw a line parallel to AG ending at point E. Line EG divides the triangle into two equal parts and both touch point G.
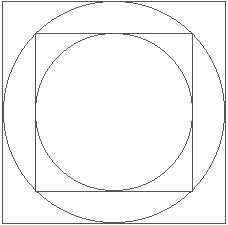
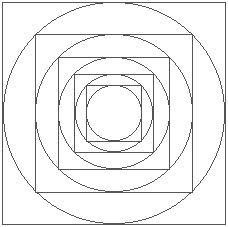
Draw a circle in a square with the diameter of the circle being equal to a side of the square. Draw another circle concentric with the first and having a diameter equal to the diagonal of the square. The second circle is twice as great in area as the first circle. Likewise, another square tangent on all sides to the greater circle is twice the area of the first square.
| | 
|
Continuing the process of drawing circles in squares, you find that the area of the outer circles and squares have a relationship of 2 to the nth power with the innermost circle and square; n being the number of circles or squares from the first circle or square.
| |
|
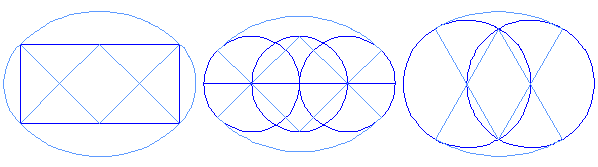
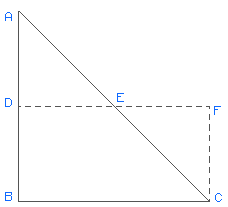
To change a right triangle into a rectangle of equal area, triangle ABC. Bisect AB and AC at their respective midpoints, creating points D and E . Extend DE until its length equals BC. This creates rectangle BCDF which is equal in area to triangle ABC.
| |
|

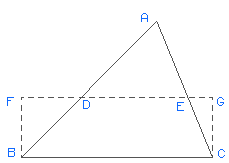
To change an irregular triangle into a rectangle of equal area, draw triangle ABC. Bisect AB and AC at their respective midpoints, creating points D and E. Extend DE until its length equals BC. This creates rectangle BCFG which is equal in area to triangle ABC.
| |
|
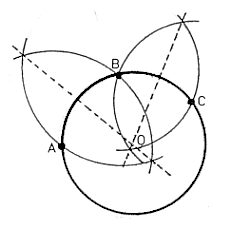
To join three points by one circle, draw three arbitrary points A, B, and C respectively. Using a compass, draw two arcs of radius AB using points A and B as center points. Repeat the process with points B and C. Draw a line through the intersections of both sets of arcs. The intersection of the two lines gives the center point of the circle that will go through points A, B, and C.
| |
|
|